Kreuztabellen und Chi-Quadrat-Analyse

Die Analyse hilft Ihnen dabei, fundierte Entscheidungen hinsichtlich Ihrer Ernährung und Ihres Kalorienverbrauchs zu treffen.

Die Kreuztabelle ist ein statistisches Modell für Großrechner, das nach ähnlichen Prinzipien funktioniert. Sie hilft Ihnen dabei, fundierte Entscheidungen hinsichtlich Ihrer Forschung zu treffen, indem sie Muster, Trends und Korrelationen zwischen Ihren Studienparametern identifiziert. Bei der Durchführung einer Studie können die Rohdaten in der Regel überwältigend sein. Sie weisen immer auf mehrere chaotische mögliche Ergebnisse hin. In einer solchen Situation hilft Ihnen die Kreuztabelle dabei, sich auf eine einzige Theorie zu konzentrieren, indem sie Trends, Vergleiche und Korrelationen zwischen sich gegenseitig einschließenden Faktoren innerhalb Ihrer Studie aufzeigt.

Nehmen wir zum Beispiel Ihre Bewerbung für die Hochschule. Damals war Ihnen das wahrscheinlich nicht bewusst, aber Sie haben mental alle relevanten Faktoren gegeneinander abgewogen, um eine bewusste Entscheidung zu treffen, welche Hochschulen Sie besuchen möchten und bei welchen Sie die besten Chancen haben. Lassen Sie uns Ihren Entscheidungsprozess Schritt für Schritt durchgehen.

Zunächst musstest du den akademischen Faktor berücksichtigen: deine Noten während der gesamten Schulzeit, deine SAT-Ergebnisse, das Fachgebiet, das du studieren möchtest, und den Bewerbungsaufsatz, den du schreiben musstest. Als zweites kommt der finanzielle Faktor, bei dem die Studiengebühren und die Möglichkeiten für ein Stipendium zu berücksichtigen sind. Zuletzt kam der emotionale Faktor hinzu, bei dem die Entfernung von zu Hause und die Entfernung zu den Universitäten, die deine Freunde in Betracht ziehen, berücksichtigt wurden, damit Treffen nicht zu einem Problem werden. Mit anderen Worten: Durch die Kreuzauswertung von akademischen Faktoren, Finanzen und Emotionen hast du eine Liste mit ausgewählten Universitäten erstellt, von denen eine deine Alma Mater ist oder bald sein wird.

Die Kreuztabelle, auch als Kreuztabelle oder Kontingenztabelle bezeichnet, ist ein statistisches Werkzeug für kategoriale Daten. Kategoriale Daten umfassen Werte, die sich gegenseitig ausschließen. Daten werden immer in Zahlen erfasst, aber Zahlen haben keinen Wert, solange sie nichts bedeuten. 4, 7, 9 sind lediglich Zahlen, sofern sie nicht näher spezifiziert sind – beispielsweise 4 Äpfel, 7 Bananen und 9 Kiwis.

Forscher verwenden Kreuztabellen, um Zusammenhänge innerhalb von Daten zu untersuchen, die nicht ohne Weiteres erkennbar sind. Dies ist besonders nützlich in Marktforschungsstudien und Umfragen. Ein Kreuztabellenbericht zeigt die Verbindung zwischen zwei oder mehr Fragen, die in der Studie gestellt wurden.

Kreuzauswertung anhand eines Beispiels verstehen

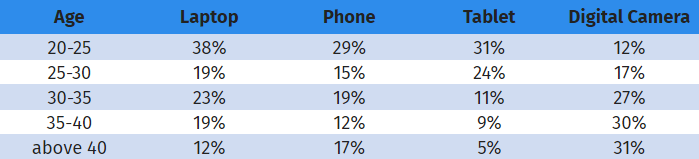
Die Kreuztabelle ist eine beliebte Wahl für die statistische Datenanalyse. Da es sich um ein Berichts-/Analysewerkzeug handelt, kann es mit jeder Datenebene verwendet werden: ordinal oder nominal. Es behandelt alle Daten als nominale Daten (nominale Daten werden nicht gemessen, sondern kategorisiert). Sie können beispielsweise die Beziehung zwischen zwei kategorialen Variablen wie Alter und Kauf von elektronischen Geräten analysieren.

Hier werden zwei Fragen gestellt:

• Wie alt bist du?

• Welches elektronische Gerät werden Sie wahrscheinlich in den nächsten sechs Monaten kaufen?

Anhand dieses Beispiels lässt sich der eindeutige Zusammenhang zwischen dem Alter und dem Kauf elektronischer Geräte erkennen. Es ist zwar nicht überraschend, aber dennoch spannend, anhand der gesammelten Daten die Korrelation zwischen diesen beiden Variablen zu sehen.

In der Umfrageforschung ermöglicht uns die Kreuztabelle eine detaillierte Analyse der potenziellen Daten, sodass Trends und Chancen leichter zu erkennen sind, ohne dass man von den aus den Antworten gesammelten Daten überwältigt wird.

Kreuztabellen und Chi-Quadrat

Der Chi-Quadrat-Test oder Pearson-Chi-Quadrat-Test ist eine statistische Hypothese, mit der Forscher feststellen können, ob es einen signifikanten Unterschied zwischen den erwarteten Häufigkeiten und den beobachteten Häufigkeiten in einer oder mehreren Kategorien gibt.

Eine wichtige Überlegung bei der Kreuztabellierung der Ergebnisse Ihrer Studie ist die Überprüfung, ob die Kreuztabellierung wahr oder falsch ist. Dies ähnelt den Zweifeln, die wir nach dem Eintritt in eine Universität haben, wenn wir uns fragen, ob dies wirklich die richtige Wahl war. Um dieses Dilemma zu lösen, wird die Kreuztabelle zusammen mit der Chi-Quadrat-Analyse berechnet, mit deren Hilfe festgestellt werden kann, ob die Variablen der Studie unabhängig voneinander sind oder miteinander in Zusammenhang stehen. Wenn die beiden Elemente unabhängig sind, wird die Tabellierung als insignifikant bezeichnet und die Studie würde als Nullhypothese bezeichnet werden. Da die Faktoren nicht miteinander in Beziehung stehen, ist das Ergebnis der Studie unzuverlässig. Im Gegensatz dazu würde eine Beziehung zwischen den beiden Elementen bestätigen, dass die Tabellierungsergebnisse signifikant sind und für strategische Entscheidungen herangezogen werden können.

Eine wichtige Überlegung bei der Kreuztabellierung der Ergebnisse Ihrer Studie ist die Überprüfung, ob die Kreuztabellierung wahr oder falsch ist. Dies ähnelt den Zweifeln, die wir nach dem Eintritt in eine Universität haben, wenn wir uns fragen, ob dies wirklich die richtige Wahl war. Um dieses Dilemma zu lösen, wird die Kreuztabelle zusammen mit der Chi-Quadrat-Analyse berechnet, mit deren Hilfe festgestellt werden kann, ob die Variablen der Studie unabhängig voneinander sind oder miteinander in Zusammenhang stehen. Wenn die beiden Elemente unabhängig sind, wird die Tabellierung als insignifikant bezeichnet und die Studie würde als Nullhypothese bezeichnet werden. Da die Faktoren nicht miteinander in Beziehung stehen, ist das Ergebnis der Studie unzuverlässig. Im Gegensatz dazu würde eine Beziehung zwischen den beiden Elementen bestätigen, dass die Tabellierungsergebnisse signifikant sind und für strategische Entscheidungen herangezogen werden können.

Ein weiterer wichtiger Begriff, den wir hier vorstellen möchten, ist die Nullhypothese. Die Nullhypothese geht davon aus, dass alle Unterschiede oder Bedeutungen, die in einem Datensatz zu erkennen sind, zufällig sind. Das Gegenteil der Nullhypothese wird als Alternativhypothese bezeichnet.

Die Anwendung des Chi-Quadrat-Tests auf Umfragen erfolgt in der Regel mit folgenden Fragetypen:

• Demografische Daten

• Likert-Skala-Fragen

• Städte

• Produktname

• Daten und Anzahl (wenn zusammengefasst)

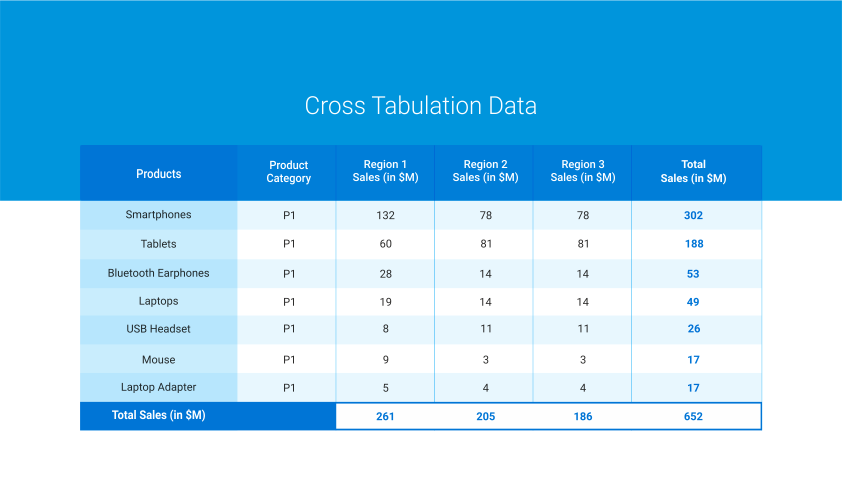
Beispielsweise möchten wir herausfinden, ob es einen Zusammenhang zwischen dem Kaufverhalten von elektronischen Geräten und der Region gibt, in der diese verkauft werden. Die Daten werden wie in der folgenden Tabelle eingegeben:

Wie bereits erwähnt, hilft Ihnen der Chi-Quadrat-Test dabei, festzustellen, ob zwei diskrete Variablen miteinander in Zusammenhang stehen. Wenn ein Zusammenhang besteht, unterscheidet sich die Verteilung einer Variablen je nach dem Wert der zweiten Variablen. Sind die beiden Variablen jedoch unabhängig voneinander, ist die Verteilung der ersten Variablen für alle Werte der zweiten Variablen gleich.

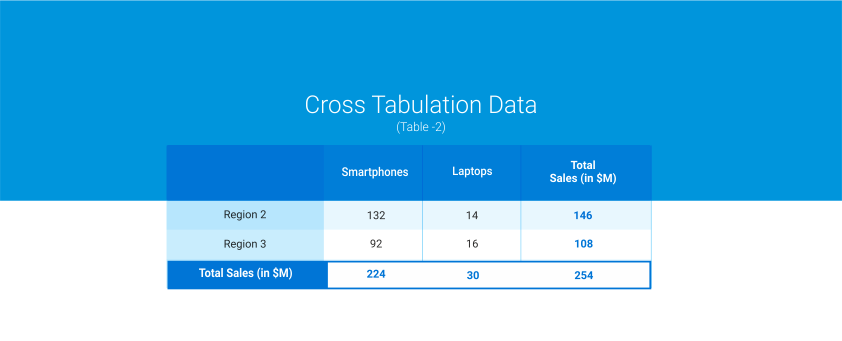
Anhand einer Kreuztabelle und des Chi-Quadrat-Tests kommen wir zu folgender Schlussfolgerung:

Anwendung der Chi-Quadrat-Berechnung auf die oben genannten Werte – Pearson-Chi-Quadrat = 0,803, P-Wert = 0,05. Was bedeutet das nun? Wir müssen auf den p-Wert achten. Vergleichen Sie den p-Wert mit Ihrem Alpha-Niveau, das üblicherweise 0,05 beträgt.

• Wenn der p-Wert kleiner oder gleich dem Alpha-Wert ist, dann sind die beiden Variablen miteinander assoziiert.

• Wenn der p-Wert größer als der Alpha-Wert ist, kommt man zu dem Schluss, dass die Variablen unabhängig sind.

In diesem Beispiel beträgt die Pearson-Chi-Quadrat-Statistik 0,803 (mit einem p-Wert von 0,05). Bei einem Alpha-Wert von 0,05 kommen wir daher zu dem Schluss, dass keine Korrelation vorliegt und diese nicht signifikant ist.

Kreuztabulation und Chi-Quadrat-Test

• Ein wesentlicher Vorteil der Verwendung von Kreuztabellen in einer Umfrage ist, dass sie einfach zu berechnen und äußerst leicht zu verstehen sind. Selbst wenn der Forscher keine fundierten Kenntnisse des Konzepts hat, lassen sich die Ergebnisse mühelos interpretieren.

• Es beseitigt Verwirrung, da Rohdaten manchmal schwer zu verstehen und zu interpretieren sind. Selbst bei kleinen Datensätzen kann es zu Verwirrung kommen, wenn die Daten nicht übersichtlich angeordnet sind. Die Kreuztabelle bietet eine einfache Möglichkeit, die Variablen miteinander in Beziehung zu setzen, wodurch Verwirrung bei der Darstellung der Daten minimiert wird.

• Aus Kreuztabellen lassen sich zahlreiche Insights ableiten. Wie in den Kreuztabellen-Beispielen im obigen Abschnitt erwähnt, ist es nicht einfach, Rohdaten zu interpretieren. Kreuztabellen stellen die Korrelation zwischen Variablen dar, sodass Insights, die sonst möglicherweise übersehen worden wären, klar verständlich werden. Selbst aus komplizierten statistischen Formen lassen sich die Insights auf einfache Weise ableiten.

• Es liefert auf einfache Weise qualifizierte oder relative Daten zu zwei oder mehr Variablen über mehrere Merkmale hinweg.

• Der wichtigste Vorteil der Verwendung von Kreuztabellen für die Analyse von Umfragen ist die einfache Verwendung beliebiger Daten, unabhängig davon, ob es sich um nominale, ordinale, Intervall- oder Verhältnismessdaten handelt.

Kreuztabulation mit QuestionPro

1. Melden Sie sich bei Ihrem QuestionPro-Konto an und wählen Sie die Umfrage aus, die Sie analysieren möchten.

2. Unter „Analytics“ finden Sie die Option „Analyse“. Klicken Sie unter „Analyse“ auf „Kreuztabelle“.

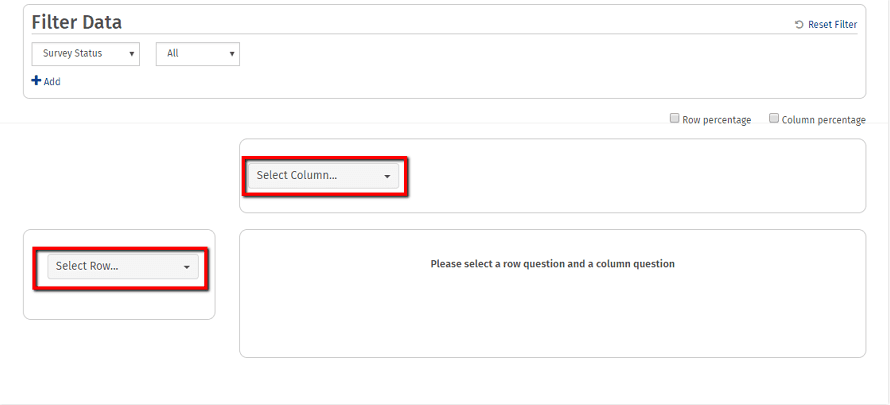
3. Wählen Sie die Frage in der Zeile und die Frage in der Spalte aus den Dropdown-Menüs aus.

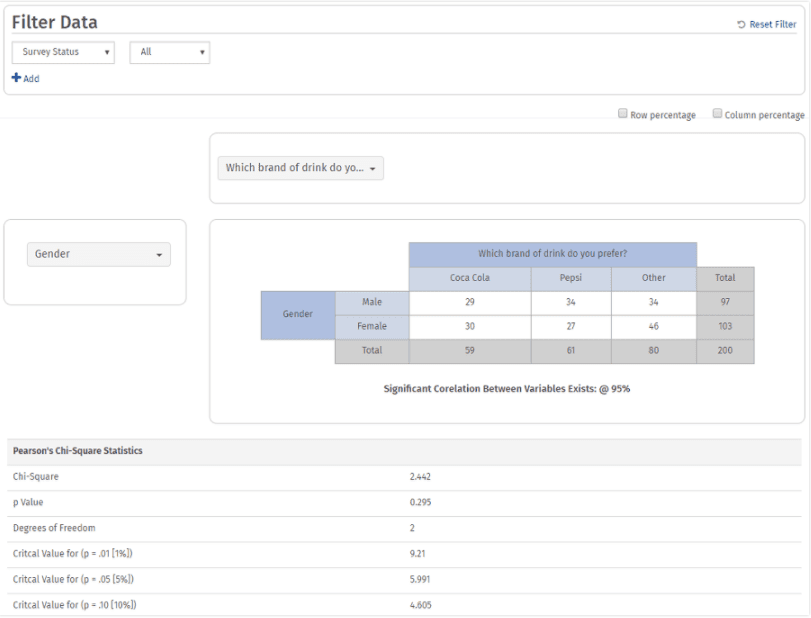
4. Eine Kreuztabelle wird zusammen mit einer Pearson-Chi-Quadrat-Analyse erstellt.

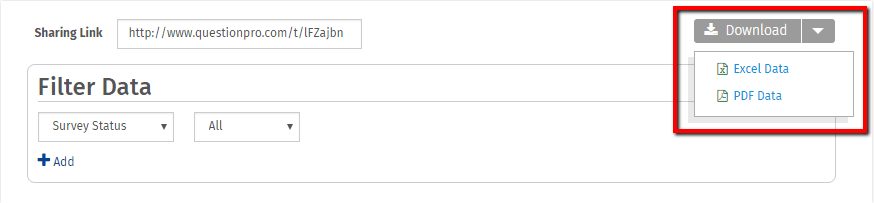
5. Nachdem Sie den Bericht erstellt haben, können Sie ihn auch herunterladen.