- Galería de imágenes
- Número de preguntas por encuesta
- Creando una encuesta desde un documento de MS Word
- Como editar encuestas en vivo
- Survey blocks
- Aleatorizador de bloques de encuestas
- Question randomization
- Scale Library
- ¿Qué son las pruebas monádicas?
- ¿Qué son las pruebas monádicas secuenciales?
- Soporte de extracción para tipos de preguntas del selector de imágenes
- ¿Qué son las pruebas de comparación?
- Mensajes de validación personalizados
- Generador de encuestas con QxBot
- Prueba de envío
- Opciones de vista previa de la encuesta
- Agregar preguntas desde un documento
- Creación de encuestas 2025
- Standard question types
- Advanced question types
- Multiple choice question type
- Text question- comment box
- Matrix multi-point scales question type
- Pregunta de orden de rango
- Pregunta de calificación de emoticones
- Image question type
- Date and time question type
- CAPTCHA question type
- Net Promoter Score question type
- Van Westendorp
- Choice modelling questions
- Side-By-Side matrix question
- Homunculus question type
- Predictive answer options
- Presentation text questions
- Multiple choice: select one
- Multiple choice: select many
- Temporizador de página
- Contact information question
- Matrix multi-select question
- Matrix spreadsheet question
- Pregunta de clasificación de tarjetas cerradas
- Flex Matrix
- Text Slider Question Type
- Pulgares arriba / abajo
- Rank Order - Drag and Drop
- Pregunta de Matriz Bipolar con escala deslizante
- Bipolar Matrix Likert Scale
- Gabor Granger
- Firma digital verificada
- Star Rating Question Type
- Push to social
- Attach Upload File Question
- Constant Sum Question
- Información sobre vídeos
- Conexión de plataforma
- TubePulse
- Clasificación de tarjetas abiertas
- Mapas Interactivos
- LiveCast
- Communities Recruitment
- tipo de respuesta
- Reorder questions
- Question tips
- Text box next to question
- Adding other option
- Matrix question settings
- image-rating-settings
- Scale options for numeric slider question
- Constant sum question settings
- Setting default answer option
- Exclusive option for multiple choice questions
- Making a question required - validation
- Bulk validation
- Remove validation message
- Question separators
- Question code
- Page breaks in survey
- Survey introduction with acceptance checkbox
- Validación de expresiones regulares
- Question Library
- Embed Media
- Posición de inicio del control deslizante
- Pantalla de respuesta Volteo alternativo
- Matriz - Modo de enfoque automático
- Validaciones de texto
- Configuración de entrada numérica: hoja de cálculo
- Grupos de respuesta
- Preguntas ocultas
- Formato de moneda del separador decimal
- Permitir varios archivos: adjuntar/cargar tipo de pregunta
- Cuadro de texto: tipo de entrada de teclado
- Bucear profundo
- Answer Display Order
- Colores alternados
- Conjoint Best Practices
- Multi-media file limits
- Conjoint Prohibited Pairs
- Text question settings
- Add logo to survey
- Custom theme using CSS
- Auto-advance
- Progress bar
- Automatic question numbering option
- Enabling social network toolbar
- Título del navegador
- Print or download survey
- Botones de navegación de la encuesta
- Tema accesible
- Atrás | Salir - Botones de navegación - ¿cómo hacerlo?
- Diseño de la encuesta
- Visual Display Mode
- Integración de Telly
- URL del espacio de trabajo
- Diseño clásico
- Display Settings
- Focus Mode
- Telly Integration
- Lógica de salto
- Lógica de ramificación compuesta
- Compound or delayed branching
- Dynamic quota control
- Texto dinámico - caja de comentarios
- Lógica de extracción
- Lógica de mostrar / ocultar pregunta
- Mostrar / ocultar dinámico
- Lógica de scoring
- Net promoter scoring model
- Piping text
- Encadenamiento de encuestas
- Looping
- Ramificación al finalizar una encuesta
- Logic operators
- Lógica N de M seleccionada
- Referencia de sintaxis lógica de JavaScript
- Block Flow
- Bloque de looping
- Scoring Engine: Syntax Reference
- Extraiga siempre y nunca extraiga la lógica
- Matrix Extraction
- Locked Extraction
- Actualización dinámica de variables personalizadas
- Advanced Randomization
- Custom Scripting Examples
- Custom Scripting
- Survey Logic Builder - AI
- Survey settings
- Guardar y continuar
- Anti Ballot Box Stuffing (ABBS) - disable multiple responses
- Deactivate survey
- Admin confirmation email
- Action alerts
- Survey timeout
- Finish options
- Spotlight report
- Print survey response
- Search and replace
- Survey Timer
- Allowing multiple respondents from the same device
- text-input-size
- Admin Confirmation Emails
- Fecha de cierre de la encuesta
- Datos de ubicación del encuestado
- Modo de revisión
- Revisar, editar e imprimir respuestas
- Geo coding
- Barra de progreso clásica | QuestionPro Help Center
- Limitación de respuestas
- Verificación de edad
- Herramientas - Opciones de encuesta
- Live survey URL
- Customize survey URL
- Create email invitation
- Personalizing emails
- Email invitation settings
- Email list filter
- Email list filter
- Survey reminders
- Export batch
- Email status
- Spam index
- Send surveys via SMS
- Phone & paper
- Adding responses manually
- Precios de SMS
- Embedding Question In Email
- Eliminar listas de correo electrónico
- Distribución de encuestas multilingües
- Mejores prácticas para envíos de correo electrónico
- SMTP
- Dirección de correo electrónico de respuesta
- Domain Authentication
- Solución de problemas de entrega de correo electrónico
- QR Code
- Entrega y capacidad de entrega de correo electrónico
- Offline app themes
- Loop survey
- Mobile app
- Kiosk mode
- Synchronize app data
- Print PDF on offline app
- Device audit
- Variables del dispositivo
- Sincronización de respuestas
- Hardware del dispositivo
- Detección de rostros en modo quiosco
- text-to-speech
- Notificación de inserción
- Buenas prácticas en la App Offline
- Survey Dashboard - Report
- Overall participant statistics
- Dropout analysis
- Banner tables
- Análisis TURF
- Análisis de tendencias
- Correlation analysis
- Survey comparison
- Gap analysis
- Mean calculation
- Weighted mean
- Spider chart
- Análisis de conglomerados
- Dashboard filter
- Opciones de descarga - Panel de control
- Análisis de puntos calientes
- Heatmap Analysis
- Orden de clasificación ponderado
- Opciones de respuesta de agrupación de tabulación cruzada
- Pruebas A/B en encuestas QuestionPro
- Data Quality
- La calidad de los datos termina
- Gráfico de mapa de calor de matriz
- Prueba de proporciones de columnas
- Identificador de respuesta
- TURF Reach Analysis
- Bulk Edit System Variables
- Ponderación - Eliminar el sesgo de la muestra
- Diseños de análisis conjoint
- Conjoint part worths calculation
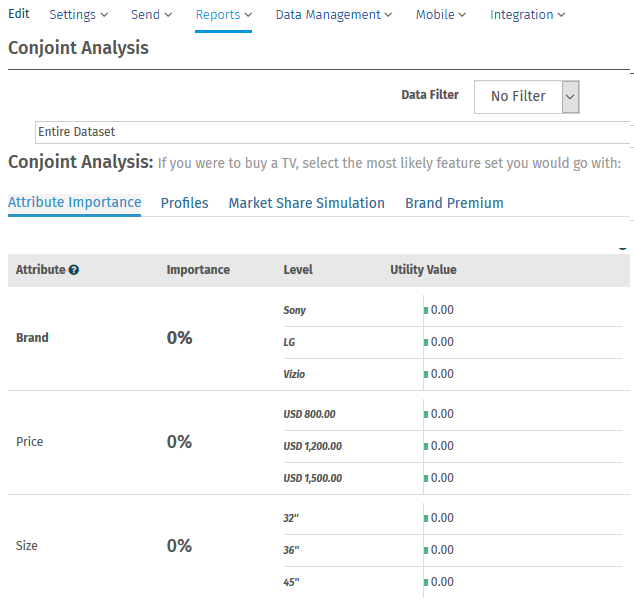
- Importancia del análisis Conjoint
- Conjoint profiles
- Market segmentation simulator
- Conjoint brand premium and price elasticity
- What is MaxDiff scaling
- MaxDiff settings
- anchored-maxdiff
- MaxDiff FAQ
- Maxdiff resultados
- Conjoint calculations and methodology
- Automatic email report
- Calidad de los datos: respuestas modeladas
- Calidad de los datos: palabras sin sentido
- Import external data
- Download center
- Consolidate report
- Delete survey data
- Calidad de los datos: todas las casillas seleccionadas
- Exporting data to Word, Excel or Powerpoint
- Scheduled reports
- Dataset
- Notification Group
- unselected-checkbox-representation
- Fusionar datos 2.0
- Deteccion de plagios
- Datos de ubicación basados en IP
- SPSS Export
- Nombre de variable de SPSS
- Update user details
- Update time zone
- Business units
- Add Users
- Usage dashboard
- Single user license
- License restrictions
- Inicio de sesión
- Software support package
- Correo electrónico de bienvenida
- Roles de usuario personalizados
- Agregar usuarios de manera masiva
- Two-Factor Authentication
- Programa de referencia de asociaciones de agencias
- Límites de respuesta
- Network Access
- Changing ownership of the survey
- Unable to access Chat support
- Navigating QuestionPro Products
Cálculo conjunto de las partes de valor
Nosotros utilizamos el siguiente algoritmo para calcular el CBC Conjunto de Valores Parciales:
- NOTACIÓN
Que haya encuestados R, con individuos r=1..R
Que cada encuestado vea tareas T, con t= 1...T
Que cada tarea T tengo configuraciones (o conceptos) C, con c = 1.. C (en nuestro caso la C normalmente es 3 o 4)
Si tenemos atributos A, a = 1 para A, con cada atributo teniendo niveles La, l = 1 para La, entonces el valor parcial es de a.
Un nivel o atributo particular es w´(a,l). Este (conjunto irregular) de los valores parciales es lo que estamos resolviendo en este ejercicio. Podemos
simplificar esto a conjunto unidimensional w(s), donde los elementos son:
{w’(1,1), w’(1,2) ... w’(1,L1), w’(2,1) ... w’(A,LA)} con w teniendo elementos S..Una configuración especifica x puede ser representada como un conjunto unidimensional x(s), donde x(s)= 1 si el
nivel o atributo especifico es presentado, de lo contrario sería 0.
Que Xrct represente la configuración especifica de la configuración cth en la tarea tth para el encuestado rth. Ademas el
diseño experimental es representado por la matriz X de cuatro dimensiones con el tamaño RxTxCxS
Si el encuestado r elije la configuración c en la tarea t, entonces deje que Yrtc=1; de lo contrario 0.
- UTILIDAD DE UNA CONFIGURACIÓN ESPECIFICA
La utilidad Ux de una configuración especifica es la suma de los valores parciales de esos niveles o atributos presentados en la configuración, es decir es el productor escalar x.w.
- MODELO MULTI-NOMIAL LOGIT
Para una elección simple entre dos configuraciones, con utilidades U1 y U2, el modelo MNL predice que la configuración 1 sera elegida.
EXP(U1)/(EXP(U1) + EXP(U2)) del tiempo (un número entre 0 y 1).
Para una elección entre N configuraciones, la configuración 1 sera elegida.
EXP(U1)/(EXP(U1) + EXP(U2) + ... + EXP(UN)) del tiempo.
- PROBALIDAD DE ELECCIÓN MODELADA
Permita que la probabilidad de elección (usando el modelo MNL) de elegir la configuración cth en la tarea tth para el encuestado rth sea:
Prtc=EXP(xrtc.w)/SUM(EXP(xrt1.w), EXP(xrt2.w), ... , EXP(xrtC.w))
- MEDIDA DE PROBABILIDAD DE REGISTRO
La medida LL de probabilidad de registro se calculada como:
Prtc es una función del valor parcial del vector w, el cual es el conjunto de valores parciales por los cuales estamos resolviendo esto.
- RESOLUCIÓN PARA LOS VALORES PARCIALES USANDO LA PROBABILIDAD MÁXIMA
Resolvemos para el vector de valor parcial, encontrando el vector w que le da el valor máximo a LL. Tome en cuenta que estamos solucionando para variables S..
Esto es un problema de maximización continuo multi-dimensional no lineal, y requiere un solucionador estándar de biblioteca. Nosotros utilizamos el algortimo simplex Nelder-Mead.
La función de probabilidad de registro debe ser implentada como una función LL(w,Y,X) y luego optimizada para encontrar el vector. Las respuestas Y y el diseño X son dadas y constantes para una optimización específica. Los valores iniciales para w pueden ser establecidos como 0.
Los ultimos valores parciales w son re definidos de manera que los valores parciales de cualquier atributo tengan una media de cero, simplemente restando el promedio de los valores parciales para todos los niveles de cada atributo.
- Login » Surveys » Reports » Choice Modelling » Conjoint Analysis